基础算法与数据结构（七） 拓扑排序

什么是拓扑排序？

拓扑排序和其他排序算法不同，它主要是给有向无环图中所有结点的一种线性排序。

依据什么排序呢？如果有一条从u指向v的边，那么u在排序结果中一定会在v前面。正因如此，所有拓扑排序只对有向无环图有效，如果图中存在任何形式的环路，那么拓扑排序将不会对其产生作用。

简而言之，拓扑排序就是一种能把图放在一条水平线上铺开的算法。

但是重要一点：

拓扑排序算法的结果可能是不同的。

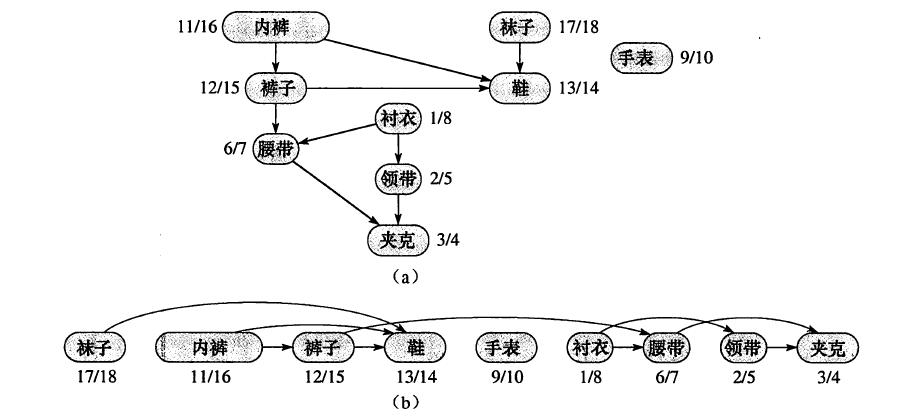
图示：某教授早上起床后的动作顺序，a为普通图，b为拓扑排序后的图。

（算法导论图22-7）

拓扑排序的算法表示

拓扑排序可以利用DFS进行，就是DFS的扩展应用，主要思想就是：

当一个结点出发的DFS完全完成之后，那么这个结点已经没有任何的后继结点可以遍历，那么这个结点就可以放在拓扑排序的结果中，结果保存在一个栈中。因为放入了栈中，其实就是放在拓扑排序的头部。（已经没有出度了）。

代码思想如下：

1、 调用dfs_travel()；

2、 在dfs_travel()每次调用dfs()的过程中，都记录了顶点s的完成时间，将顶点s按完成顺序保存在存放拓扑排序顺序的栈topoSort中。这样，该数组就存放了按先后顺序访问完成的所有顶点。

3、 最后拓扑排序得到的线性序列，即为topoSort。

talk is cheap:(代码前提，没有环，可能有环的情况见例题）

stack<int> tpsort;
vector<vector<int>> graph;
bool visited[graph.size()];
void TP(){
	int size = graph.size();
	for(int i = 0;i<size;i++){
		if(!visited[i]) dfs(i);
	}
}

void dfs(int x){
	if(visited[x]) return;
	for(int i=x+1;i<size;i++){
		if(graph[x][i]) dfs(i);
	}
	tpsort.push(x);
	return;
}

例题

LeetCode 207 Course Schedule

这道题就是拓扑排序的简化版，其实只要用一次DFS即可，主要考点就是拓扑排序中不能有环存在，检测环要记录这一次DFS走过的路径才可以，所以每次走完DFS后，cycle中其实是空的。只要用DFS检测出环，即可判断为false

这道题卡时间，不能用邻接矩阵做，一定要用unordered_set。莫名其妙在时间上卡了好久，思路其实很简单。

其实也可以用BFS做，可以参见LeetCode中Solution中的代码，解释的也很详尽。

上代码

class Solution {
public:
    
    bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
        if(prerequisites.empty()) return true;
        vector<unordered_set<int>> graph(numCourses);
        
        int size = prerequisites.size();
        for(int i=0;i<size;i++){
            graph[prerequisites[i].second].insert(prerequisites[i].first);
        }
        unordered_set<int> visited;
        vector<bool> flag(numCourses, false);
        for(int i = 0;i<numCourses;i++){
            if(!flag[i])
                if(DFS(graph,visited,i,flag)) 
                    return false;
        }
        return true;
    }
    
    
    bool DFS(vector<unordered_set<int>> &matrix, unordered_set<int> &visited, int b, vector<bool> &flag){
    flag[b] = true;
    visited.insert(b);
    for(auto it = matrix[b].begin(); it != matrix[b].end(); ++ it)
        if(visited.find(*it) != visited.end() || DFS(matrix, visited, *it, flag))
            return true;
    visited.erase(b);
    return false;
}
};

LeetCode 210 Course Schedule II

这道题就是上一道题的强化版，也是正宗的拓扑排序，利用visited判断是否访问过进行排序，cycle判断是否有环存在。每次递归前吧现在位置加入cycle，如果再次回到了之前访问过的地方，那么存在环，就无法拓扑排序了。道理和上一道题是一样的。

之所以不能重用visited来判断环的存在，因为visited会表示之前一次DFS所存储下来的走过的路径值，会导致判断错误。

这道题卡时间没有上一题紧。

上代码

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<pair<int, int>>& prerequisites) {
        vector<int> ans;
        vector<unordered_set<int>> graph(numCourses);
        
        for(int i=0;i<prerequisites.size();i++){
            graph[prerequisites[i].second].insert(prerequisites[i].first);
        }
        vector<bool> visited(numCourses);
        unordered_set<int> cycle;
        for(int i=0;i<numCourses;i++){
            if(!visited[i]){
                if(!dfs_sort(ans,i,visited,graph,cycle)){
                    ans.clear();
                    return ans;
                }
            }
        }
        reverse(ans.begin(),ans.end());
        return ans;
    }
    
    bool dfs_sort(vector<int>& ans,int x,vector<bool>& visited,vector<unordered_set<int>>&graph,unordered_set<int>& cycle){
        if(visited[x]) return true;
        visited[x] = true;
        cycle.insert(x);
        for(auto it = graph[x].begin();it!=graph[x].end();++it ){
            if(cycle.find(*it) != cycle.end() || !dfs_sort(ans,*it,visited,graph,cycle)) return false;
        }
        cycle.erase(x);
        ans.push_back(x);
        return true;
    }
};