基础算法与数据结构(十二) 简单排序算法
排序算法
今天开始,将进入一个新的领域,各种各样的排序算法。
排序算法可以用一本TAOCP分册的篇幅来讲述,这里肯定不能全部讲到。
今天主要来写一点简单基础的排序算法。
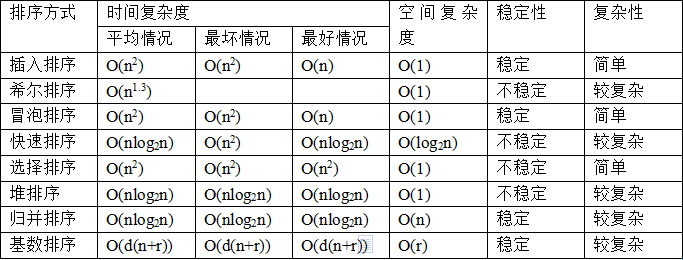
排序算法的时间复杂度
一般来讲基于比较来排序的算法,最快的时间复杂度为O(nlgn)。
来给出一些常见排序算法的时间复杂度:
本文里将一起讲述插入排序、选择排序、冒泡排序、归并排序和希尔排序5种排序算法。
一些代码的共用部分
排序算法一般来说都需要进行比较和交换位置,有一些代码进行复用。
1
2
3
4
5
6
7
8
9
public boolean less(Comparable v, Comparable w){
return v.compareTo(w) < 0;
}
public void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
插入排序
描述
插入排序简单来说,和理牌的方式基本一致,一个一个向后扫描,将一个未排序的数组元素向前插入到一个合适的位置,然后将其余所有元素向后移一个位置。
情况分析
最坏的情况,就是要排序的数组完全倒序,需要的移动次数最多,如果接近已经排序了,那么插入排序的移动次序较少。
一些趣闻
插入排序需要的交换操作和数组中倒置的数量相同,需要的比较次数大于等于倒置的数量,小于等于倒置的数量加上数组的大小减一。
Java实现
1
2
3
4
5
6
7
8
9
10
public class Insertion{
public static void sort(Comparable[] a){
int N = a.length;
for(int i = 1;i<N;i++){
for(int j = i;j>0 && less(a[j],a[j-1]);j--){
exch(a,j,j-1);
}
}
}
}
选择排序
描述
首先,找到数组中最小的那个元素,其次,将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。
再次,再剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。
Java实现
1
2
3
4
5
6
7
8
9
10
11
12
public class Selection{
public static void sort(Comparable[] a){
int N = a.length;
for(int i = 0;i<N;i++){
int min = i;
for(int j = i+1;j<N;j++){
if(less(a[j],a[min]) min = j;
}
exch(a,i,min);
}
}
}
冒泡排序
描述
冒泡排序算是一个比较经典的排序法了。首先从队首取一个元素,向后寻找,直到找到一个比它小的元素,然后交换位置之后,再从第二个元素开始循环上述的方式,直到所有的元素排完序。
Java实现
1
2
3
4
5
6
7
8
9
10
11
public class Bubble{
public static void sort(Comparable[] a){
int N = a.length;
for(int i = 0;i<N;i++){
int cur = i;
for(int j = i+1;j<N;j++){
if(less(a[cur],a[j]) exch(a,cur,j);
}
}
}
}
归并排序
描述
归并排序其实在第一次链表的时候就已经讲到了。归并排序就是一个二分法的应用。
归并排序将两个有序的数组归并成一个更大的有序数组。也就是将一个数组排序,可以先递归地将它分成两半分别排序,然后将归并起来。可以得到比之前的几个排序算法更好的时间复杂度。
归并排序的几种方式
- 原地归并
- 自顶向下
- 自底向上
原地归并的实现方式
原地归并就是创建一个新的数组,然后将排完序之后的内容放回到原数组中,也是另外两个的基础归并的方式。
1
2
3
4
5
6
7
8
9
10
11
12
13
public static void merge(Comparable[] a,int lo,int mid, int hi){
int i = lo, j=mid+1;
for(int k = lo;k <= hi;k++){
aux[k] = a[k];
}
for(int k = lo;k<=hi;k++){
if( i > mid ) a[k] = aux[j++];
else if(j > hi) a[k] = aux[i++];
else if(less(aux[j],aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
该方法将所有的元素复制到aux中,然后在归并到a中。
用了4个条件判断进行排序的下一步判断。
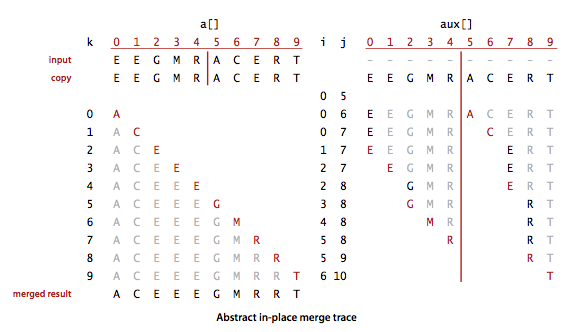
原地归并的图示: 摘选自 《算法(第4版)》
自顶向下的归并排序
1
2
3
4
5
6
7
8
9
10
11
12
public static void sort(Comparable[] a){
aux = new Comparable[a.length];
sort(a,0,a.length-1);
}
public static void sort(Comparable[] a,int lo,int hi){
if(hi<=lo) return;
int mid = lo + (hi-lo)/2;
sort(a, lo , mid); //排左半边
sort(a, mid+1, hi); //排右半边
merge(a, lo, mid, hi);
}
图示:
自底向上的归并排序
1
2
3
4
5
6
7
8
9
10
public static Comparable[] aux;
public static void sort(Comparable[] a){
int N = a.length;
aux = new Comparable[N];
for(int sz = 1;sz<=N;sz = sz+sz){
for(int lo = 0;lo<N-sz;lo+=sz +sz){
merge(a,lo,lo+sz-1,Math.min(lo+sz+sz-1,N-1);
}
}
}
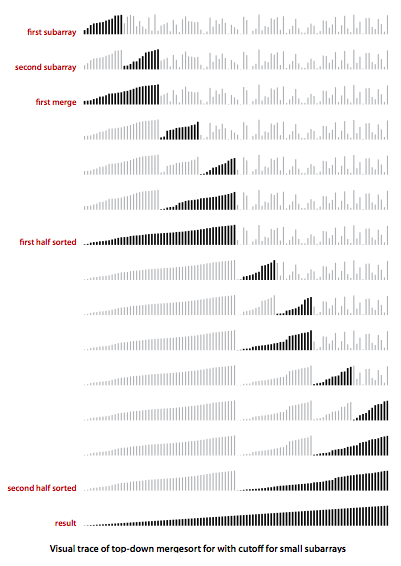
运行轨迹图示:
最后来一个可视化的运行轨迹。
希尔排序
描述
希尔排序是一个基于插入排序的快速的排序算法。插入排序只能交换相邻的元素,希尔排序为了加快速度简单的改进了插入排序,交换不相邻的元素已对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。
希尔排序的思想是使数组中任意间隔为h的元素是有序的,这样的数组被称为h有序数组。一个h有序数组就是h个相互独立的有序数组编制在一起组成的一个数组。如果h很大,我们就能将元素移动到很远的地方。
希尔排序就是利用h递增来进行排序。
java代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void sort(Comparable[] a){
int N = a.length;
int h = 1;
//找到最大的h,从大到小进行h排序
while(h < N/3) h = 3*h + 1;
while(h >= 1){
//将数组变为h有序
for(int i = h;i<N;i++){
//将a[i]插入到a[i-h],a[i-2*h],a[i-3*h]...之中
for(int j = 1;j>=h && less(a[j],a[j-h]);j-=h){
exch(a,j,j-h);
}
}
h = h/3;
}
}
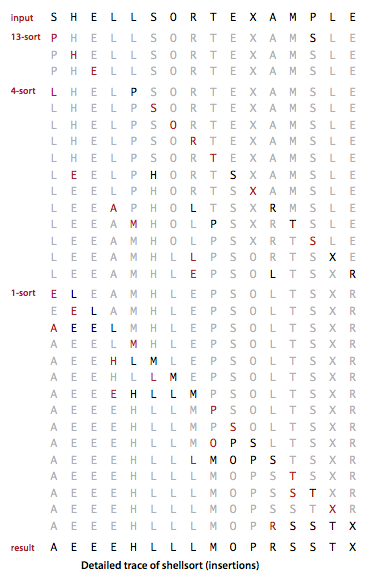
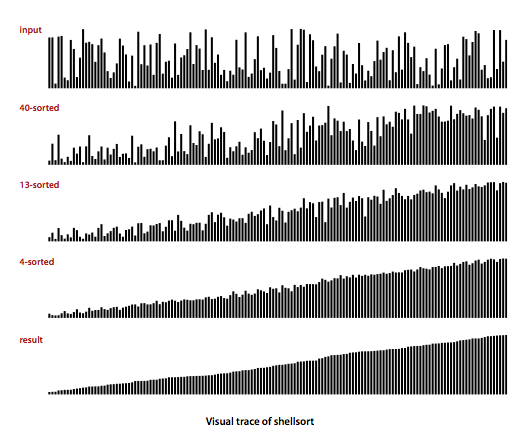
希尔排序的几张图,第一个是h有序数组的图示: