基础算法与数据结构(四) 树(3)平衡二叉树之红黑树
本文中所有与红黑树有关的代码均来自于刘新宇所著《算法新解》中的红黑树章节。
平衡二叉树
根据之前的表述,因为二叉树可能为退化为链表,所以产生了平衡二叉树这个产物,主要为了避免在插入值的时候产生退化的问题。
平衡二叉树主要有两种实现方式,一种是红黑树,一种是AVL树。首先先复习红黑树。
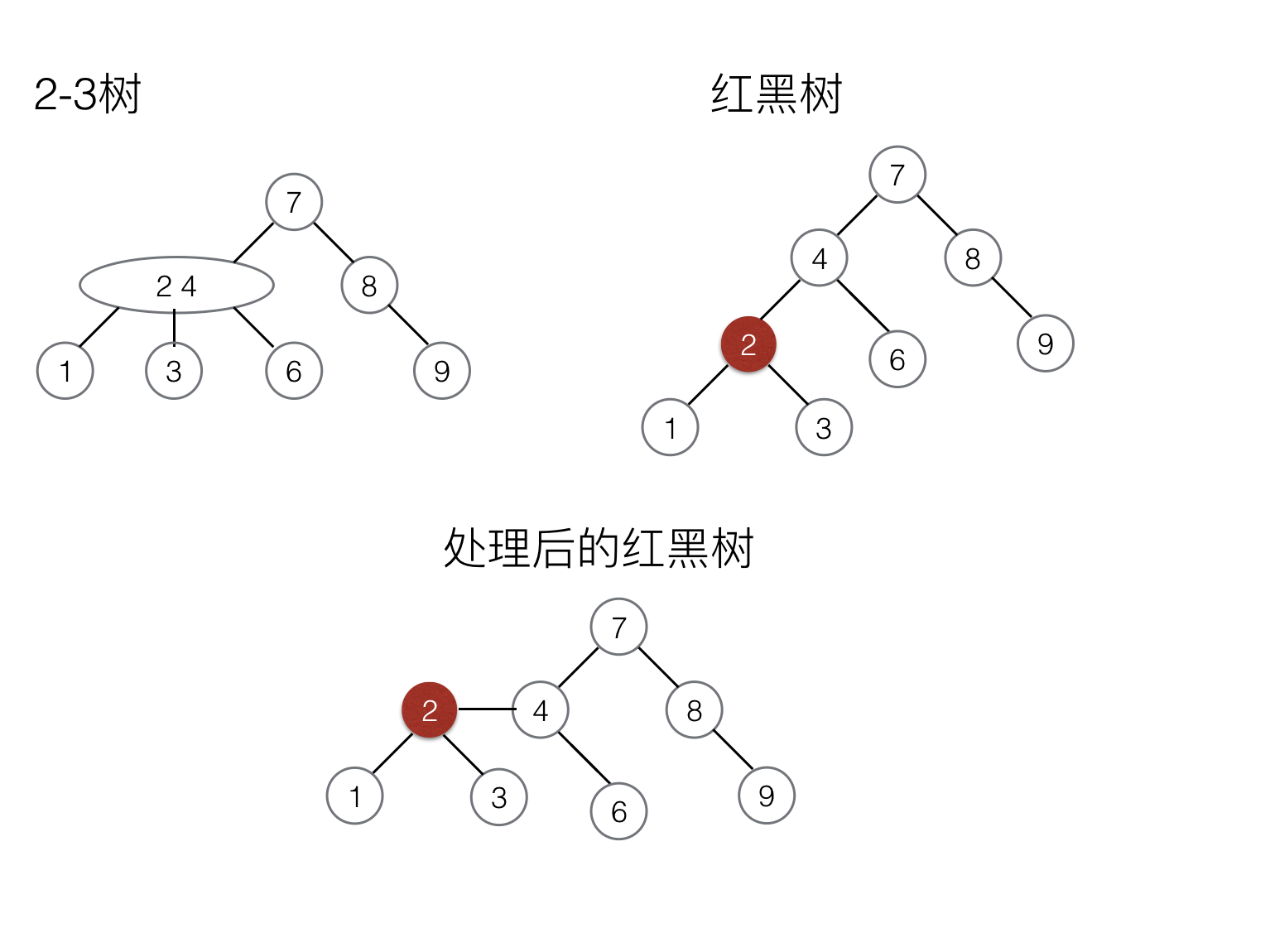
2-3树
在介绍红黑树之前,先介绍一种理想的平衡二叉树 — 2-3树
2-3树有两种节点,分别是2结点和3结点,分别定义如下: * 2结点:含有一个键(和其对应的值)和两条链接,左链接指向2-3树种的键都小于该结点,右链接指向的2-3树中的键都大于该结点。(即一般的二叉树节点) * 3结点:含有两个键(和其对应的值)和三条链接,左链接指向的2-3树种的键都小于该节点,中链接指向的2-3树种的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。 * 指向一颗空树的连接称为空链接。
一棵完美平衡的2-3查找树中的所有空链接到根节点的距离都是相同的。
2-3树的增删改查
查询
类似于一般二叉树中的查找,根据结点的key值和要查找的key值进行比较,递归相应的子树进行查询。
插入
由于结点的不同,这里有几种插入的情况:
向一棵只含有一个3结点的树中插入新结点: 先创建一个4-结点(定义类似于2结点等),然后将其转换为两个只含有2-结点的子树。中间数成为根节点,另外两个成为对应的左右子树。
向一个父节点为2-结点的3-结点插入新结点: 先在3-结点中创建为4-结点,然后将中间值移向作为父节点的2-结点,将父节点改为3-结点,新创建的两个链接,分别指向剩余的两个结点。
向一个父节点为3-结点的3-结点插入新节点: 一路向上变为4-结点追溯,只到出现2-结点,利用2进行变换。如果最后将根节点变为了3-结点,那么就要对这个3-结点进行分解,利用1后半段的方法即可。
红黑树
在了解2-3树之后,理解红黑树的定义就会稍稍简单一点。。。
- 利用2-3树延伸出红黑树: 红结点与上一层的黑结点一起组成了一个3结点,所以不可能出现两个红结点连续出现的情形。
如图所示:
- 定义:红黑树是一种自平衡二叉搜索树。通过对节点进行着色和旋转,红黑树很容易保持树的平衡。(有一种版本是对节点之间的连接进行红黑分类,这里使用节点红黑)
- 性质:
- 任一节点要么是红色,要么是黑色。
- 根节点为黑色。
- 所有的叶节点为黑色。(叶节点为最后的nil节点为黑色,并非传统意义上的最底层结点,一般都满足。)
- 如果一个节点为红色,那么两个子节点都是黑色。
- 对任一节点,从他出发到所有叶子节点的路径上包含相同数量的黑色节点。 从根节点出发到达叶节点的所有路径中,最长路径不会超过最短路径的2倍。
- 红黑树的节点数据结构
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55
struct Node { Key key; Color color; Node* left; Node* right; Node* parent; Node(Key k, Color c = Color::RED) : key(k), color(c), left(nullptr), right(nullptr), parent(nullptr) {} virtual ~Node() { delete left; delete right; } void setLeft(Node* x) { left = x; if (x) x->parent = this; } void setRight(Node* x) { right = x; if (x) x->parent = this; } void setChildren(Node* x, Node* y) { setLeft(x); setRight(y); } // parent <--> this ==> parent <--> y void replaceWith(Node* y) { if (!parent) { if (y) y->parent = nullptr; } else if (parent->left == this) { parent->setLeft(y); } else { parent->setRight(y); } parent = nullptr; } Node* sibling() { return parent->left == this ? parent->right : parent->left; } Node* uncle() { return parent->sibling(); } Node* grandparent() { return parent->parent; } };
树的旋转操作
即在保持树的中序遍历结果不变的情况下,改变树的结构。
树的左右旋操作的C++代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//left rotation: (a, x, (b, y, c)) ==> ((a, x, b), y, c)
Node* leftRotate(Node* t, Node* x) {
Node* parent = x->parent;
Node* y = x->right;
Node* a = x->left;
Node* b = y->left;
Node* c = y->right;
x->replaceWith(y);
x->setChildren(a, b);
y->setChildren(x, c);
if (!parent) t = y;
return t;
}
// right rotation: (a, x, (b, y, c)) <== ((a, x, b), y, c)
Node* rightRotate(Node* t, Node* y) {
Node* parent = y->parent;
Node* x = y->left;
Node* a = x->left;
Node* b = x->right;
Node* c = y->right;
y->replaceWith(x);
y->setChildren(b, c);
x->setChildren(a, y);
if (!parent) t = x;
return t;
}
红黑树中的增删查操作
查询操作
可以类似于一般的二叉树进行递归的查询操作,时间复杂度在O(lgn)
1
2
3
4
5
Node* search(Node* t, Key x) {
while (t && t->key != x)
t = x < t->key ? t->left : t->right;
return t;
}
插入操作
插入操作是红黑树中最复杂的实现之一,需要在一般二叉树的插入操作基础上进行红黑变换以及树的旋转才能够正确插入,需要调整的情况主要会有2种(基本2种,考虑左右对称有4种)。
插入操作的前半部分就是一般的二叉树插入操作,找到应该插入的位置,并且声明一个红色结点。由于红结点不能相邻,所以会有需要调整的情况。
(为什么初始化为红色结点? 因为性质中规定从根节点到所有叶子节点上需要有相同数量的黑色节点,所以要有节点变黑,就要两边都变黑,否则不可。(这一点很重要)如果初始化为黑色节点会破坏这个性质。)
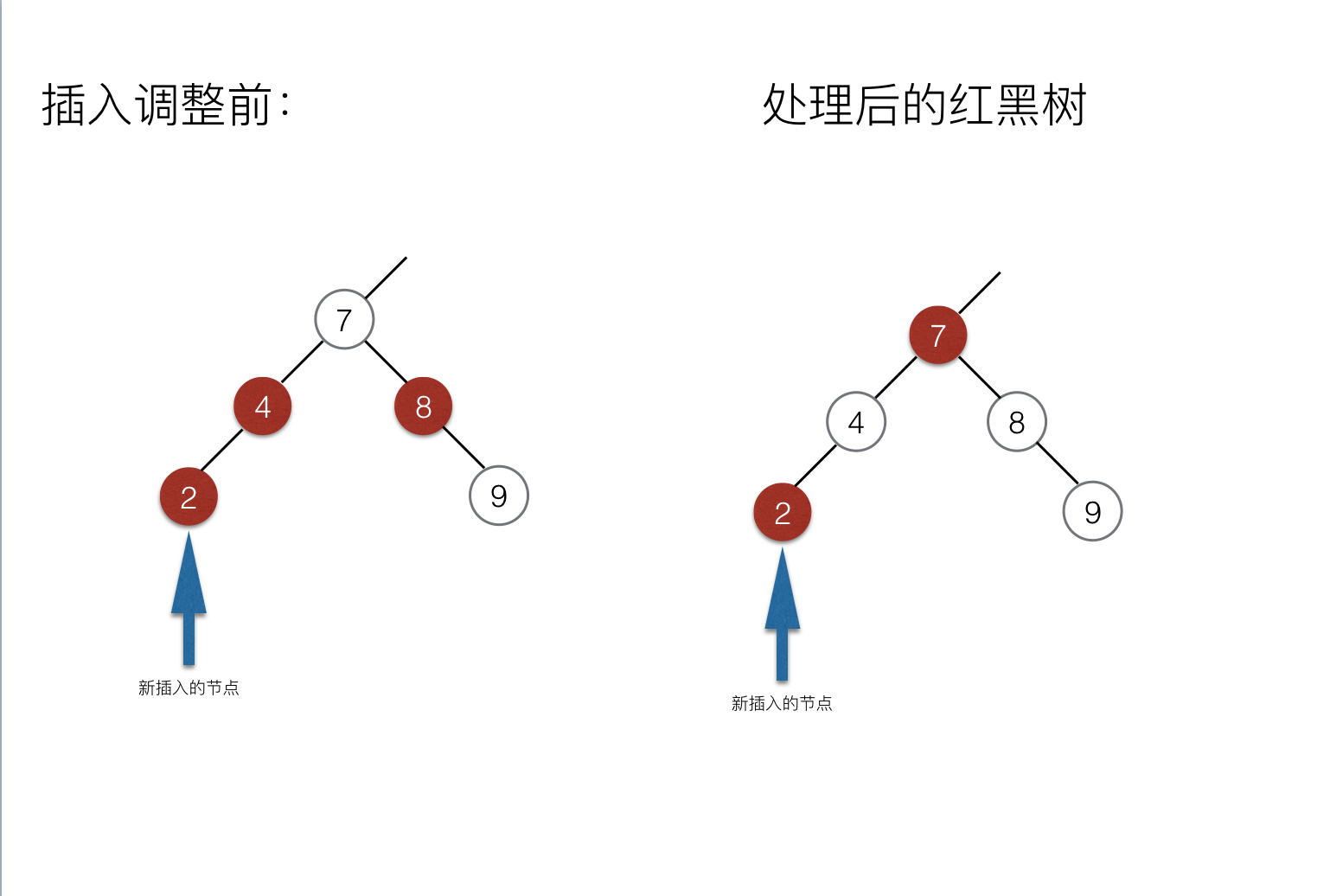
情况一: 插入节点的父节点和父节点的兄弟结点均为红色。 此时的解决方案就是把父节点和父节点的兄弟结点变为黑色,同时将祖父结点变为红色,此时并不会改变这棵红黑树所展现的平衡性质。 如果此时祖父节点变为红色之后又产生了两个相邻的红色结点,那么只需要在进行一次相同操作即可,直到这棵树最后平衡。
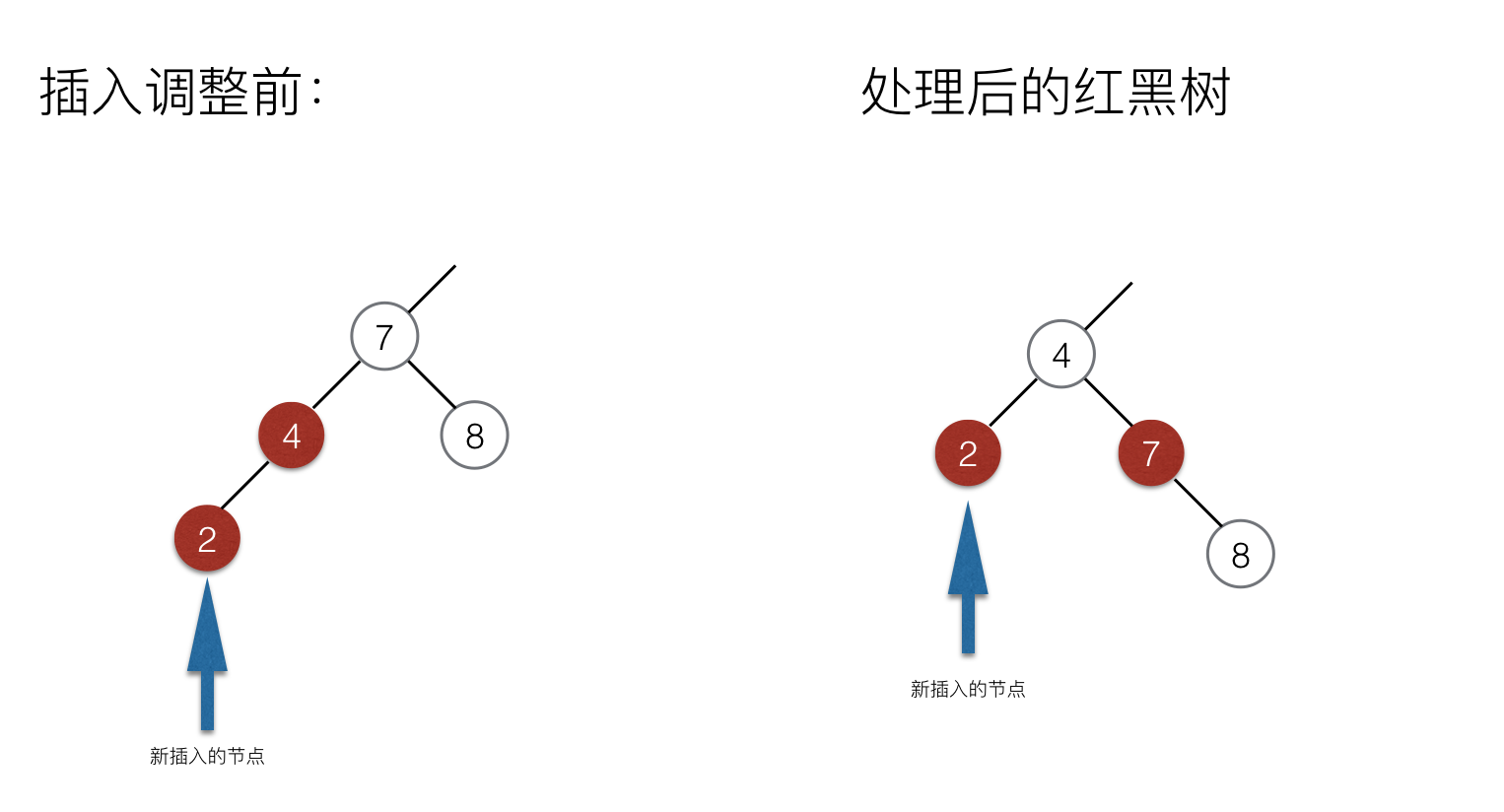
情况二:插入节点的父节点为红色,而父节点的兄弟结点为黑色
这个情况比之前复杂,因为不能直接将父节点染黑了,所以要对整棵树进行旋转操作才能够满足红黑树的5条性质。
如果插入的是在左边位置,那么就将整棵树以祖父节点右旋,将原先的红结点变为“大家长”,可以进行染黑操作了,消除了两个红结点相邻,并且不会增加黑结点数目。那么原先的祖父节点变为了右子树,由于原先祖父节点为黑结点,需要转为红结点才能保持平衡。
上图:
最后只需要进行根节点的判断进行红黑转换即可。
上代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// returns the new root,normal insert
Node* insert(Node* t, Key key) {
Node* root = t;
Node* x = new Node(key);
Node* parent = nullptr;
while (t) {
parent = t;
t = key < t->key ? t->left : t->right;
}
if (!parent) { //insert key to the empty tree
root = x;
} else if (key < parent -> key) {
parent->setLeft(x);
} else {
parent->setRight(x);
}
return insertFix(root, x);
}
// fix the red->red violation
Node* insertFix(Node* t, Node* x) {
while (x->parent && x->parent->color == Color::RED) {
if (x->uncle()->color == Color::RED) {
// case 1: ((a:R, x:R, b), y:B, c:R) ==> ((a:R, x:B, b), y:R, c:B)
setColors(x->parent, Color::BLACK,
x->grandparent(), Color::RED,
x->uncle(), Color::BLACK);
x = x->grandparent();
} else {
if (x->parent == x->grandparent()->left) {
if (x == x->parent->right) {
// case 2: ((a, x:R, b:R), y:B, c) ==> case 3
x = x->parent;
t = leftRotate(t, x);
}
// case 3: ((a:R, x:R, b), y:B, c) ==> (a:R, x:B, (b, y:R, c))
setColors(x->parent, Color::BLACK,
x->grandparent(), Color::RED);
t = rightRotate(t, x->grandparent());
} else {
if (x == x->parent->left) {
// case 2': (a, x:B, (b:R, y:R, c)) ==> case 3'
x = x->parent;
t = rightRotate(t, x);
}
// case 3': (a, x:B, (b, y:R, c:R)) ==> ((a, x:R, b), y:B, c:R)
setColors(x->parent, Color::BLACK,
x->grandparent(), Color::RED);
t = leftRotate(t, x->grandparent());
}
}
}
t->color = Color::BLACK;
return t;
}
删除操作
我手边的所有资料基本都将最复杂的删除操作作为了练习。确实,删除操作复杂点就在删除黑结点的同时会产生破坏性质5的结果,需要进行调整。
不过由于二叉搜索树在实际应用中,如果需要删除超过一半的节点,不如重新建树罢了。
删除操作可以参考https://juejin.im/entry/58371f13a22b9d006882902d 里的讲解。
平衡树的典型例题
LeetCode 108 利用排完序的数组重建二叉树。 两种解法: 1. 利用分治法分别建左右树 2.利用平衡树的旋转等操作进行平衡,如果直接插入会导致退化。
待补充。