基础算法与数据结构（十三） 快速排序

本节所有图片均选自 https://algs4.cs.princeton.edu/23quicksort/

快速排序

今天讲述的是一般语言自带的模板排序算法也是应用最广泛的排序算法— 快速排序。

并不是说他最快，而是一般情况下它的性能能够达到普遍最优。

它仅靠一个辅助栈以及NlgN的时间效率，是其他算法所无法结合的两个优点。

快速排序描述

快速排序是一种分治的排序算法，它将一个数组分为两个子数组，当两个自数字都有序的时候，整个数组自然有序。

快速排序的精髓就在于切分。

快速排序的切分

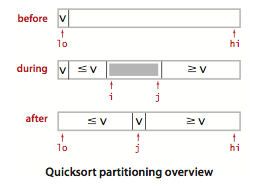
首先这是一个切分的示意图。

切分的整个过程中满足下面三个条件：

1. 对于某个j，a[j]已经排定。
2. a[lo] 到 a[j-1]的所有元素都不大于a[j]
3. a[j+1]到a[hi}的所有元素都不小于a[j]

一般的策略如下

先随意的去a[lo]作为切分元素，即那个将会被排定的元素。 然后从数组的左端开始向右扫描直到找到一个大于等于它的元素，再从数组的右端开始向左扫描直到找到一个小于等于它的元素，将这两个元素交换。 一直找到两个方向的扫描相遇，这一次的切分结束。

切分完毕并不保证切分元素的左右各自有序，只能保证切分元素左半侧，切分元素，切分元素右侧这个大方向上有序，具体的有序还要基本算法去递归排序。

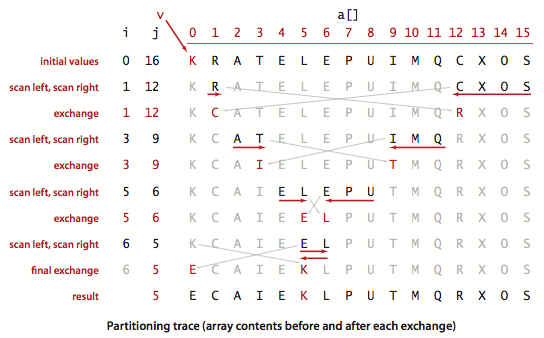
轨迹就如下图所示：

切分的实现代码：（Java）

public int partition (Comparable[] a,int lo,int hi){
	int i = lo,j = hi+1;
	//将数组分为a[lo..i-1],a[i],a[i+1...hi]
	Comparable v = a[lo]; //切分元素
	while(true){
		while(less(a[++i],v)) if(i == hi) break;
		while(less(v,a[--j])) if(j == lo) break;
		if(i>=j) break;
		exch(a,i,j);
	}
	exch(a,lo,j);   //把切分元素放回中间
	return j;   //返回切分元素的位置
}

基本算法

写完切分，接下来真正进入快速排序的算法部分了，其实切分完了快速排序也就完成了四分之三了。

算法的基本思路就是切分当前部分，把大于切分元素和小于切分元素的元素分开，剩下的在进行排序。

到了最底层，就可以保证元素直接都是有序的。

这个其实也就是归并排序的反过来思考。

Java算法代码：

public class QuickSort{
	public void sort(Comparable[] a,int lo,int hi){
		if(hi <= lo) return;
		int j = partition(a,lo,hi);
		sort(a, lo, j-1);
		sort(a, j+1, hi);
	}
}

快速排序的精髓就在之前的切分，递归切分就能通过数学归纳法证明整体有序了。

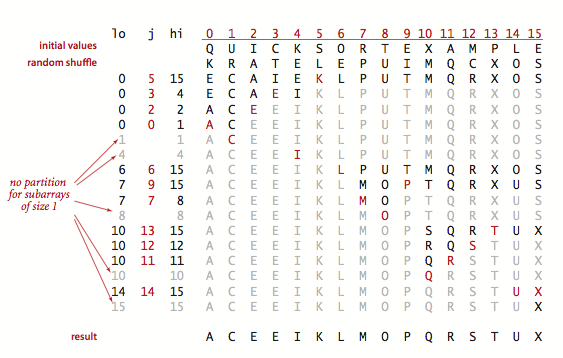
快速排序运行图：

基本算法的几个细节问题

1. 别越界
2. 终止循环条件
3. 处理切分元素值有重复的情况。
4. 要把元素放入到正确位置然后终止递归。

快速排序的继续改进

通过三向快速排序可以继续改进这个快速排序，具体可以参见算法（第4版）这本书。