基础算法与数据结构(六) 图与其基础算法
图的基础概念
- 图的定义: 无向图: 一个图G = (V,E)由顶点(或结点)的非空集V和边的集合E构成,每条边有一个或两个顶点与它相连,这样的顶点称为端点。边连接它的端点。(顶点集为无限的称为无限图,反之称为有限图)
有向图:一个有向图(V,E)由一个非空顶点集V和一个有向边集E组成。每条有向边与一个顶点有序对相关联。与有序对(u,v)相关联的有向边开始于u,结束于v
- 图的离散数学概念速览 本文重点不是离散数学,这里只提供一些名词供查漏补缺只用。 顶点的度,入度,出度,孤立的顶点,连通性,连通分量,强连通,完全图,二分图 。。。。。。
图的数据结构表示
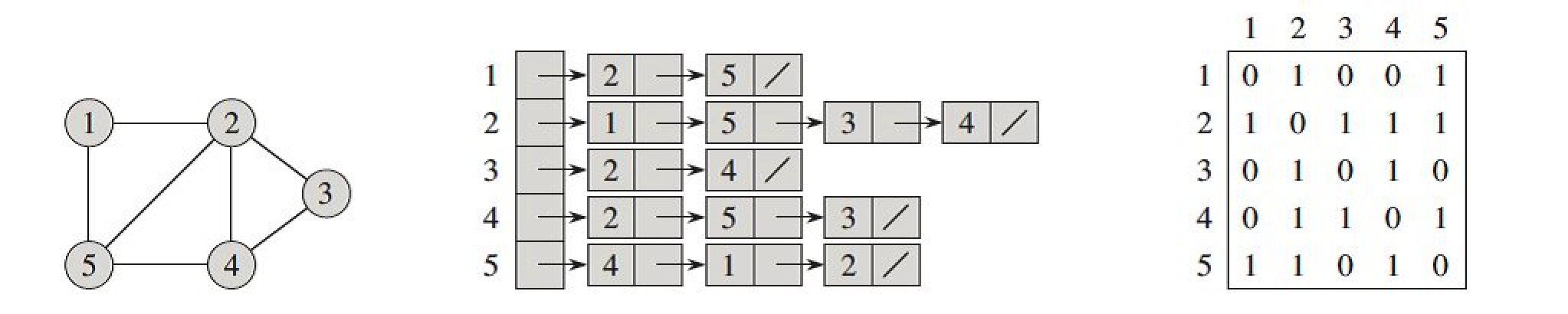
一个图可以利用两种方式来表示,一种是邻接矩阵,另一种为邻接链表。
邻接矩阵
用一个二维数组可以表现一个图,数组中A[i][j]表示从i到j是否有一条连通的边,有则为1,无则为0。 缺点是存储所需要的空间较大,为顶点个数的平方级别,对存储空间要求较大,但查询方便。
邻接链表
用一个指针数组来表示。A[i]链表表示从i号点能够到达的结点号。这种方式可以节省存储空间,但是查询并不是很方便。
两种方法都容易用代码实现,此略。
广度优先算法(BFS)
虽然把广度优先算法放在图这里,但是也可以用于树,后文给出的一道题就是树上的BFS运用。
广度优先算法用语言通俗表述就是,一层一层向外扩展,在距离起点相同距离的点走完之前不想外扩展。
广度优先算法可以求出源点到所有点的最短路径。
广度优先算法的代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//邻接矩阵版
void BFS(vector<vector<int>> graph){
int size = graph.size();
bool visited[size];
queue<int> que;
que.push(0); //从0开始遍历
while(!que.empty()){
int curPoint = que.front();
que.pop();
visited[curPoint] = true;
for(int i = 0;i<size;i++){
if(graph[curPoint][i] && visited[i]){
que.push(y);
//对这条链路的操作,如果求距离,在这里把距离+1等。
}
}
}
}
//邻接表版
void BFS(vector<GraphNode*> graph,int size){
bool visited[size];
queue<GraphNode*> que;
que.push(graph[0])
while(!que.empty()){
GraphNode* cur = que.front();
que.pop();
visited[curPoint] = true;
GraphNode* next = cur->next;
while(next){
if(visited[next->No]){
que.push(next);
}
}
}
}
深度优先搜索(DFS)
深度优先搜索就是一次性走到不能走,再往回走,知道走完所有的路。 是回溯法的典型应用,就可以利用递归快速理解和解决。
一般可以用来解决一些关于图连通的问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
bool visited[size];
vector<vector<int>> graph;
int size = graph.size();
void DFS(){
visited[x][y] = true;
for(int i = 0;i<size;i++){
for(int j = 0;j<size;j++){
if(!visited[i][j]){
DFS(i,j);
}
}
}
}
典型题
DFS和BFS的思想可以利用到很多题目上,题目不胜枚举,LeetCode上也有很多可以训练,择其典型者列出。
BFS
LeetCode 102 Binary Tree Level Order Traversal 据说是面试常考题,也是BFS的典型题,重点就在BFS一层一层向下的思想。
上代码:(此处为JAVA代码)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
if(root==null) return ans;
bfs(root);
return ans;
}
void bfs(TreeNode root){
//Set<TreeNode> visited = new HashSet<>();
//如果是图一定需要visited!!!!(因为这里是树,所以可以省略)
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
//visited.add(root);
while(!queue.isEmpty()){
int levelSize = queue.size();
//得到上一层究竟放入了多少结点,因为在退出循环前之前放入的已经完全访问过,并且出队列。
List<Integer> levelNodes = new ArrayList<>();
while(levelSize-- >0){
TreeNode curNode = queue.poll();
levelNodes.add(curNode.val);
if(curNode.left != null) queue.add(curNode.left);
if(curNode.right != null) queue.add(curNode.right);
}
ans.add(levelNodes);
}
}
DFS
LeetCode 200 Number of Islands 图连通性的典型题目,也是可以利用DFS的典型题目。
每一次的DFS可以根据四连通走遍所有可以连通的,并且标记visited。 退出后就是找到一个岛。
然后再在途中照可以连通但并没有访问过的节点在进行DFS操作。
如此循环往复,最后全部访问过以后,走过几遍DFS就是有多少岛
上代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//四连通的坐标变化
int[] dx = {-1,0,1,0};
int[] dy = {0,-1,0,1};
int row;
int col;
boolean[][] visited;
char[][] gridx;
public int numIslands(char[][] grid) {
if(grid.length == 0) return 0;
gridx = grid;
row = grid.length;
col = grid[0].length;
visited = new boolean[row][col];
int cnt = 0;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(!visited[i][j] && gridx[i][j] == '1'){
dfs(i,j);
cnt++;
}
}
}
return cnt;
}
void dfs(int i,int j){
if(visited[i][j]) return;
visited[i][j] = true;
for(int p=0;p<4;p++){
int x = i+dx[p];
int y = j+dy[p];
//防止溢出
if(x>=0 && x<row && y>=0 && y<col && gridx[x][y] == '1' )
dfs(x,y);
}
}